Вітаємо!
Ми, група теоретиків 8-А класу КЗШ №122, працюючи в рамках проекту з математики
"Цей знайомий і незнайомий Піфагор"
досліджували питання:
Чи є межі досконалості доведення "піфагорових штанів"?
Об'єктом дослідження: Теорема ПіфагораЗадачі, що стояли перед нашою групою:
- Вивчення математичної літератури, ресурсів Інтернету;
- Знаходження максимальної кількості способів доведення теореми Піфагора;
- Систематизація зібраного матеріалу;
- Класифікація методів доведення
Результати досліджень наша група відтворює на сторінці даного блогу. Будимо раді, якщо Вам згодяться ці матеріали. Нам вони допомогли урізноманітнити прийоми доведення тверджень, попробувати свої сили в створені способу доведення; впевнитись в тому, що меж досконалості доведення теореми не має. Будимо вдячні, якщо Ви запропонуєте свій спосіб доведення теореми Піфагора і надішлите на наш блог
Доведення, що базуються на використанні рівновеликості фігур з яких вони складаються.
Метод паралелограмів
Нехай A,B, C — вершини прямокутного трикутника, з прямим кутом A. Опустимо перпендикуляр з точки A на сторону, протилежну до гіпотенузи в квадраті, побудованому на ній. Лінія ділить квадрат на два прямокутники кожен з яких має таку саму площу, що й квадрати, побудовані на катетах. Головна ідея при доведенні полягає в тому, що верхні квадрати перетворюються на паралелограми такої самої площі, а тоді повертаються і перетворюються на прямокутники в нижньому квадраті і знову при незмінній площі.
Для формального доведення, нам необхідні чотири елементарні леми:
- Якщо дві сторони одного трикутника і кут між ними дорівнюють відповідно двом сторонам та куту між ним іншого трикутника, то такі трикутники рівні (сторона-кут-сторона).
- Площа трикутника дорівнює половині площі паралелограма, що має таку саму основу і таку саму висоту.
- Площа прямокутника дорівнює добутку двох суміжних сторін.
- Площа квадрата дорівнює добутку двох його сторін (випливає з третьої леми).
Тоді кожен верхній квадрат пов'язаний з трикутником, конгруентним з іншим трикутником, який пов'язаний поворотом з одним із двох прямокутників, що утворюють нижній квадрат.
Перейдемо до доведення:
Нехай ACB — прямокутний трикутник з прямим кутом CAB.
На кожній стороні BC, AB, і CA побудуємо квадрати CBDE, BAGF та ACIH в такому ж порядку. Побудова квадратів тут же вимагає попередньої теореми Евкліда, і залежить від постулату паралельності.
З точки A проводимо пряму паралельну до BD і CE. Вона перпендикулярно перетне відрізки BC та DE в точках K та L, відповідно.
Проведемо відрізки CF і AD, отримаємо трикутники BCF і BDA.
Кути CAB і BAG — прямі; відповідно точки C, A і G — колінеарні. Так само B, A і H.
Кути CBD і FBA — обидва прямі; тоді кут ABD дорівнює куту FBC, оскільки обидва є сумою прямого кута та кута ABC.
Трикутники ABD та FBC рівні за двома сторонами та кутом між ними.
Оскільки точки A, K і L — колінеарні, площа прямокутника BDLK дорівнює двом площам трикутника ABD (BDLK = BAGF= AB2)
Аналогічно міркуючи, отримаємо CKLE = ACIH = AC2
З одного боку площа CBDE дорівнює сумі площ прямокутників BDLK та CKLE, а з другого боку площа квадрата BC2, абоAB2 + AC2 = BC2.
Метод площ
Доведення Гарфілда
Sтрапеції=1/2(a+b)(a+b)Sтрикутників=1/2ab+1/2ab+1/2c2
1/2(a+b)(a+b)=1/2ab+1/2ab+1/2c2
Після спрощення
а2+b2=c2
Спрощене доведення Евкліда
Нехай квадрат, побудований на одному з катетів (на малюнку це квадрат, побудований на більшому катеті), розташований з тієї ж сторони катета, що і сам трикутник. Тоді продовження протилежного катету сторони цього квадрата проходить через вершину квадрата, побудованого на гіпотенузі. Досить порівняти площі фігур, що нас цікавлять з площею одного трикутника (він заштрихований) - площа цього трикутника дорівнює половині площі квадрата і одночасно половині площі прямокутника
Метод подібності
Нехай ABC — прямокутний трикутник, в якому кут C прямий, як показано на малюнку. Проведемо висоту з точки C, і назвемо H точку перетину з стороною AB. Утворений трикутник ACH подібний до трикутника ABC, оскільки вони обидва прямокутні (за визначенням висоти), і в них спільний кут A, очевидно третій кут буде в цих трикутників також однаковий. Аналогічно міркуючи, трикутник CBH також подібний до трикутникаABC. З подібності трикутників: Якщо
BC=a, AC=b, AB=c, тоді a/c=HB/a, b/c=AH/b
Це можна записати у вигляді a2 =c*HB, b2 =c*AH
Якщо додати ці дві рівності, отримаєм
Іншими словами, Теорема Піфагора:
Метод побудови
Доведення Гофмана
Побудуємо
трикутник АВС з прямим кутом С
Побудуємо відрізок
BF рівний CB, BF перпендикулярний CB
Побудуємо BE рівний AB, BE перпендикулярний AB
Побудуємо AD рівний AC, AD перпендикулярний AC
Точки F, C, D належать
одній прямій
Так як
чотирикутники ADFB и ACBE рівновеликі,
т. Трикутники ABF і ЕCB рівні. Трикутники ADF і
ACE рівновеликі
Віднімемо від
обох рівновеликих чотирикутників спільний для них трикутник АВС, отримаємо:
1/2а2+1/2b2=1/2c2
а2+b2=c2
Алгебраїчний метод
Маємо 0,5ab=0,5pr=0,5(a+b+c)·0,5(a+b-c)
Доведення Мьольманна
Площа даного трикутника з однієї сторони дорівнює 1/2ab, а з другої - 1/2pr, де р - півпериметр, r- радіус вписаного кола. В прямокутному трикутнику r=1/2(a+b-c).Маємо 0,5ab=0,5pr=0,5(a+b+c)·0,5(a+b-c)
0,5ab=0,5(a+b+c)·0,5(a+b-c)
аb=0,5(a2 + ab – ac + ab + b2 – bc + ca + cb - c2)
аb=0,5(a2 +b2- c2 +2ab)/·2
2аb=a2 +b2- c2 +2ab
a2 + b2- c2 =0
Розташуємо чотири однакові прямокутні трикутники так, як це зображено на малюнку.
Чотирикутник зі сторонами c є квадратом, оскільки сума двох гострих кутів  , а розгорнутий кут —
, а розгорнутий кут — 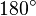 .
.
 , а розгорнутий кут —
, а розгорнутий кут — 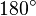 .
.
Площа всієї фігури рівна, з одної сторони, площі квадрата зі стороною «a+b», а з іншої — сумі площ чотирьох трикутників і внутрішнього квадрата.
Доведення теореми через косинус кута
Нехай АВС — даний прямокутний трикутник з прямим кутом С. Проведемо висоту CD з з вершини прямого кута С.
По означенню косинуса кута (Косинусом гострого кута прямокутного трикутника називається відношення прилеглого катета до гіпотенузи) соsА=AD/AC=AC/AB. Звідси AB*AD=АС2 Аналогічно соsВ=BD/BC=BC/AB. Звідси AB*BD=ВС2. Додаємо почленно дві рівності. Так як AD+DB=AB, маємо:
Теорема доведена
По означенню косинуса кута (Косинусом гострого кута прямокутного трикутника називається відношення прилеглого катета до гіпотенузи) соsА=AD/AC=AC/AB. Звідси AB*AD=АС2 Аналогічно соsВ=BD/BC=BC/AB. Звідси AB*BD=ВС2. Додаємо почленно дві рівності. Так як AD+DB=AB, маємо:
Теорема доведена
АС2+ВС2=АВ(AD + DB)=АВ2.
Векторний метод
Нехай АВС - прямокутний трикутник з прямим кутом С, побудований на векторах. Тоді справедлива векторна рівність
a = c + b;
c = a - b;
c²=a²+b²-2 a b; Так як a перпендикулярний b , то a b= 0.
c²=a²+b²
Адитивний метод (метод розкладу)
Існує цілий ряд доведень теореми Піфагора, в яких квадрати, побудовані на катетах і на гіпотенузі, розрізають так, що кожної частини квадрата, побудованого на гіпотенузі, відповідає частина одного з квадратів, побудованих на катетах. У всіх цих випадках для розуміння докази достатньо одного погляду на креслення; міркування тут може бути обмежене єдиним словом: "Дивись!", Як це робилося в творах стародавніх індуських математиків. Слід, однак, зауважити, що насправді доказ можна вважати повним, поки ми не довели рівності всіх відповідних один одному частин. Це майже завжди досить важко зробити, однак може (особливо при великій кількості частин) зажадати досить тривалої роботи.
Доведення Епштейна
Тут в якості складових частин розкладання фігурують виключно трикутники. Щоб розібратися в кресленні, зауважимо, що пряма CD проведена перпендикулярно прямий EF.
Розкладання на трикутники можна зробити і більш наочним, ніж на малюнку.
Розкладання на трикутники можна зробити і більш наочним, ніж на малюнку.
Доведення Нільсена
На малюнку допоміжні лінії змінені за пропозицією Нільсена.
Доведення Бетхера
На малюнку дано досить наочне розкладання Бетхер.
Доведення Перігаля
У підручниках нерідко зустрічається розкладання зазначене на малюнку (так зване "колесо з лопатями"; це доказ знайшов Перігаль). Через центр O квадрата, побудованого на більшій катета, проводимо прямі, паралельну і перпендикулярну гіпотенузі. Відповідність частин фігури добре видно з креслення
Доведення Гутхейля
Зображене на малюнку розкладання належить Гутхейль; для нього характерне наочне розташування окремих частин, що дозволяє відразу побачити, які спрощення спричинить за собою випадок рівнобедреного прямокутного трикутника.
Метод віднімання
Знайомий нам малюнок теореми Піфагора укладемо в прямокутну рамку, напрямки сторін якої збігаються з напрямками катетів трикутника. Продовжимо деякі з відрізків фігури так, як вказано на малюнку, при цьому прямокутник розпадається на кілька трикутників, прямокутників і квадратів. Викинемо з прямокутника спочатку кілька частин так щоб залишився лише квадрат, побудований на гіпотенузі. Ці частини наступні:
трикутники 1, 2, 3, 4;
прямокутник 5;
прямокутник 6 і квадрат 8;
прямокутник 7 і квадрат 9;
Потім викинемо з прямокутника частини так, щоб залишилися тільки квадрати, побудовані на катетах. Цими частинами будуть:
прямокутники 6 і 7;
прямокутник 5;
прямокутник 1 (заштрихований);
прямокутник 2 (заштрихований);
Нам залишилося лише показати, що відібрані частини рівновеликі. Це легко бачити в силу розташування фігур. З малюнка ясно, що:
прямокутник 5 рівновеликий самому собі;
чотири трикутника 1,2,3,4 рівновеликі двом прямокутникам 6 і 7;
прямокутник 6 і квадрат 8, взяті разом, рівновеликі прямокутнику 1 (заштрихований);;
прямокутник 7 разом з квадратом 9 рівновеликі прямокутнику 2 (заштрихований).
трикутники 1, 2, 3, 4;
прямокутник 5;
прямокутник 6 і квадрат 8;
прямокутник 7 і квадрат 9;
Потім викинемо з прямокутника частини так, щоб залишилися тільки квадрати, побудовані на катетах. Цими частинами будуть:
прямокутники 6 і 7;
прямокутник 5;
прямокутник 1 (заштрихований);
прямокутник 2 (заштрихований);
Нам залишилося лише показати, що відібрані частини рівновеликі. Це легко бачити в силу розташування фігур. З малюнка ясно, що:
прямокутник 5 рівновеликий самому собі;
чотири трикутника 1,2,3,4 рівновеликі двом прямокутникам 6 і 7;
прямокутник 6 і квадрат 8, взяті разом, рівновеликі прямокутнику 1 (заштрихований);;
прямокутник 7 разом з квадратом 9 рівновеликі прямокутнику 2 (заштрихований).
Метод доповнення
Загальна ідея таких доказів полягає в наступному.
Від двох рівних площ потрібно відняти рівновеликі частини так, щоб в одному випадку залишилися два квадрати, побудовані на катетах, а в іншому-квадрат, побудований на гіпотенузі. Адже якщо в рівностях
В-А = С і В1-А1 = С1
частина А рівновелика частини А1, а частина В рівновелика В1, то частини С і С1 також рівновеликі.
На класичному рисунку до теореми Піфагора приставлені зверху і знизу трикутники 2 і 3, рівні вихідному трикутнику 1. Пряма DG обов'язково пройде через C. Зауважимо тепер (далі ми це доведемо), що шестикутники DABGFE і CAJKHB рівновеликі. Якщо ми від першого з них віднімемо трикутники 1 і 2, то залишаться квадрати, побудовані на катетах, а якщо від другого шестикутника віднімемо рівні трикутники 1 і 3, то залишиться квадрат, побудований на гіпотенузі. Звідси випливає, що квадрат, побудований на гіпотенузі, рівновеликий сумі квадратів, побудованих на катетах.
Залишається довести, що наші шестикутники рівновеликі. Зауважимо, що пряма DG ділить верхній шестикутник на рівновеликі частини; те саме можна сказати про прямий CK і нижньому шестикутнику. Повернемо чотирикутник DABG, що становить половину шестикутника DABGFE, навколо точки А за годинниковою стрілкою на кут 90; тоді він співпаде з чотирикутником CAJK, складовим половину шестикутника CAJKHB. Тому шестикутники DABGFE і CAJKHB рівновеликі.
Від двох рівних площ потрібно відняти рівновеликі частини так, щоб в одному випадку залишилися два квадрати, побудовані на катетах, а в іншому-квадрат, побудований на гіпотенузі. Адже якщо в рівностях
В-А = С і В1-А1 = С1
частина А рівновелика частини А1, а частина В рівновелика В1, то частини С і С1 також рівновеликі.
На класичному рисунку до теореми Піфагора приставлені зверху і знизу трикутники 2 і 3, рівні вихідному трикутнику 1. Пряма DG обов'язково пройде через C. Зауважимо тепер (далі ми це доведемо), що шестикутники DABGFE і CAJKHB рівновеликі. Якщо ми від першого з них віднімемо трикутники 1 і 2, то залишаться квадрати, побудовані на катетах, а якщо від другого шестикутника віднімемо рівні трикутники 1 і 3, то залишиться квадрат, побудований на гіпотенузі. Звідси випливає, що квадрат, побудований на гіпотенузі, рівновеликий сумі квадратів, побудованих на катетах.
Залишається довести, що наші шестикутники рівновеликі. Зауважимо, що пряма DG ділить верхній шестикутник на рівновеликі частини; те саме можна сказати про прямий CK і нижньому шестикутнику. Повернемо чотирикутник DABG, що становить половину шестикутника DABGFE, навколо точки А за годинниковою стрілкою на кут 90; тоді він співпаде з чотирикутником CAJK, складовим половину шестикутника CAJKHB. Тому шестикутники DABGFE і CAJKHB рівновеликі.
Метод геометричних перетворень
Метод Хоукінса
Прямокутний трикутник ABC з прямим кутом C повернемо на 90 ° так, щоб він зайняв положення трикутника A'CB '. Продовжимо гіпотенузу A'В 'за точку A' до перетину з лінією АВ в точці D. Відрізок В'D буде висотою трикутника В'АВ. Розглянемо тепер заштрихований чотирикутник A'АВ'В. Його можна розкласти на два рівнобедрених трикутника САA 'і СВВ' (або на два трикутники A'В'А і A'В'В).
S(CAA ')= b ² / 2
S(CBB ')= a ² / 2
S(A'AB'В) = (a ² + b ²) / 2
Трикутники A'В'А і A'В'В мають загальну основу і висоти DA і DB, тому:
S(A'AB'B) = c * DA / 2 + c * DB / 2 = c (DA + DB) / 2 = c ² / 2
Порівнюючи два отриманих вирази для площі, отримаємо:
a ² + b ² = c ²
Існує багато доказів теореми Піфагора, проведених як кожним з описаних методів, так і за допомогою поєднання різних методів.
Використані джерела
Я пізнаю світ. Дитяча енциклопедія. Математика. М.1997
Энциклопедия для детей. Математика. Главный редактор М.Д.Аксенова. М. "Аванта +", 1998
Энциклопедический словарь юного математика./Сост. А.П.Савин. М. Педагогика - Пресс. 1997
Глейзер Г.И. История математики в школе. М. Просвещение, 1981
М.И.Бурда, Н.А.Тарасенкова Геометрия 8
Використані джерела
Я пізнаю світ. Дитяча енциклопедія. Математика. М.1997
Энциклопедия для детей. Математика. Главный редактор М.Д.Аксенова. М. "Аванта +", 1998
Энциклопедический словарь юного математика./Сост. А.П.Савин. М. Педагогика - Пресс. 1997
Глейзер Г.И. История математики в школе. М. Просвещение, 1981
М.И.Бурда, Н.А.Тарасенкова Геометрия 8









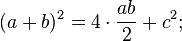
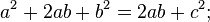













для шкільного проєкту занадто не крєатівнєнько
ВідповістиВидалити